Statistiken beim erfolgreichen Bridgespiel: die Kenntnis von statistischen Informationen spielt beim Bridge eine entscheidende Rolle. Auf dieser Seite geht es um Wahrscheinlichkeiten bei Kartenverteilungen, um die Spieltechnik bei fehlenden Figuren und wie sich Wahrscheinlichkeiten verändern, wenn zusätzliche Informationen aus der Reizung und aus dem Spielverlauf bekannt sind. Die gezeigten Tabellen stammen von der Webseite Bridgehands.
Neben Bridgehands gibt es im englischsprachigen Raum eine Reihe weiterer Quellen für Statistikinformationen:
- Bridge probabilities: Verteilung fehlender Karten; Wahrscheinlichkeit eines Fits in einer Partnerschaft; Wahrscheinlichkeit eines Schnappers durch den Gegner, abhängig von der Zahl der ausstehenden Karten.
- Contract bridge probabilities auf Wikipedia: Wahrscheinlichkeit für die Verteilung der Figuren; Anzahl möglicher Hände; Verliererzählung
Verteilung fehlender Karten
Wenn in einer Farbe Karten fehlen, dann bestehen bestimmte Wahrscheinlichkeiten für die Verteilung der fehlenden Karten beim Gegner.
Beispiel: Fehlen 6 Karten in einer Farbe, dann hat eine 3-3 Verteilung beim Gegner eine Wahrscheinlichkeit von 35,5% und eine 4-2 Verteilung eine Wahrscheinlichkeit von 48,5%.
Generell gilt, dass bei einer geraden Zahl von fehlenden Karten die Wahrscheinlichkeit für eine ungleiche Verteilung höher ist, als für eine gleiche Verteilung. Bei einer ungeraden Zahl von fehlenden Karten geht man davon aus, dass sie möglichst gleich verteilt sind.
Die Daten der folgenden Tabelle stammen von der Webseite Bridgehands.

“a posteriori” Wahrscheinlichkeiten
Wenn im Verlauf des Spiels zusätzliche Informationen über die Kartenverteilung von Nebenfarben beim Gegner bekannt sind, benutzen Spieler das „a posteriori“ Konzept, um die ursprüngliche Einschätzung der Kartenverteilung zu revidieren.
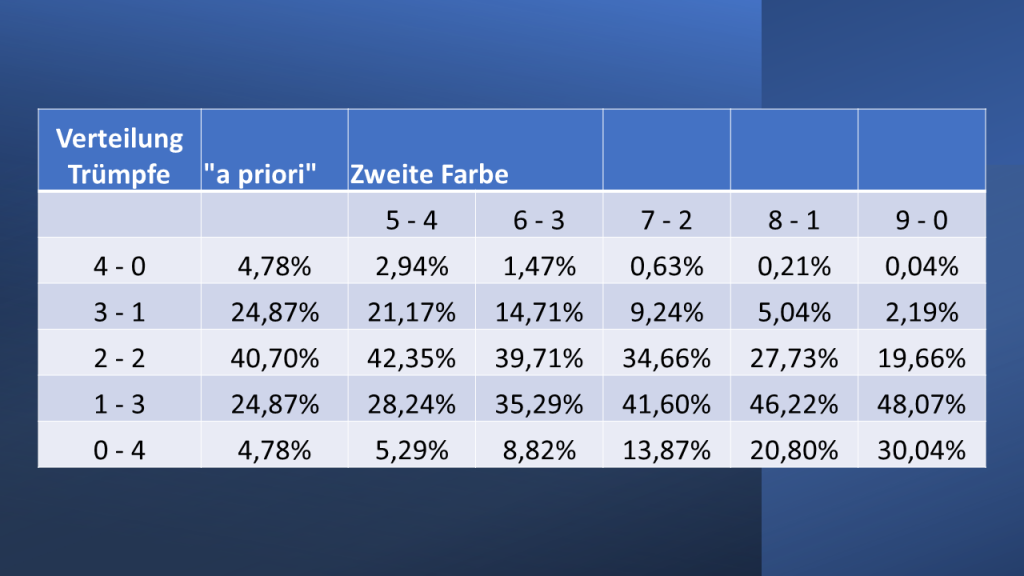
Beispiel: Die Gegner halten 4 Karten in der Trumpffarbe. Die Wahrscheinlichkeit für eine 2-2 Verteilung dieser Karten ist ursprünglich 40,7% und für eine 3-1 Verteilung 24,87%. Wenn wir jedoch aus der Reizung oder aus dem Spielverlauf wissen, dass ein Gegner eine große Zahl von Karten in einer anderen Farbe hält, dann hat dieser Gegner weniger „freie Plätze“ für Karten in der Trumpffarbe. Hat er beispielweise 7 Karten in einer Nebenfarbe, sinkt die Wahrscheinlichkeit für eine 2-2 Verteilung der Trümpfe auf 34,66% und die Wahrscheinlichkeit für eine 3-1 Verteilung der Trümpfe beim anderen Gegner steigt auf 41,6%.
Die folgende Tabelle von Bridgehands zeigt die geänderten Wahrscheinlichkeiten auf Basis der zusätzlichen Informationen:
Stichpotential und Spielweise abhängig von den fehlenden Figuren
Wenn in einer Farbe Figuren fehlen, hängt die beste Spielweise davon ab, wie viele Karten man in dieser Farbe hat und wie diese Karten verteilt sind. Zusätzlich kann die Spielweise auch davon abhängen, wie viele Stiche man benötigt. In der folgenden Tabelle kann man durch einen Klick auf die jeweils zutreffende Situation zu einer großen Anzahl von Beispielen gelangen. Es wird auch die Wahrscheinlichkeit für die Anzahl der möglichen Stiche und die beste Spielweise gezeigt. Dabei wird vorausgesetzt, dass keine zusätzlichen Informationen aus der Reizung oder dem Spielverlauf bekannt sind und dass genügend Übergänge bestehen.
Im beiliegenden Dokument sind einige Beispiele zur Wahrscheinlichkeit für eine bestimmte Anzahl von Stichen bei typischen Kartenverteilungen aufgeführt.
Die Daten der folgenden Tabellen stammen von der Webseite Bridgehands. Leider sind die Informationen nicht fehlerfrei. Ich habe versucht, diese Fehler nach bestem Wissen zu beseitigen. Die angegebenen Prozente für die jeweilige Stichzahl konnten von mir nicht überprüft werden.
Sollten Sie einen Fehler in den Tabellen entdecken, wäre ich für einen Hinweis sehr dankbar.
Beispiel: Fehlen König und Bube in einer Farbe hängt es von der Länge und Verteilung der eigenen Karten ab, wie man am besten spielt. Die optimale Spielweise hängt auch davon ab, wie viele Stiche man benötigt. In der Tabelle wird auch angezeigt, wie hoch die Wahrscheinlichkeit für die jeweilige Anzahl von Stichen ist.

Fehlende Punkte
0
1
2
3
4
5
6
7
8
9
Fehlende Figuren
Fehlende Figuren
–
–
–
–
–
Verteilung der Karten in einer Hand
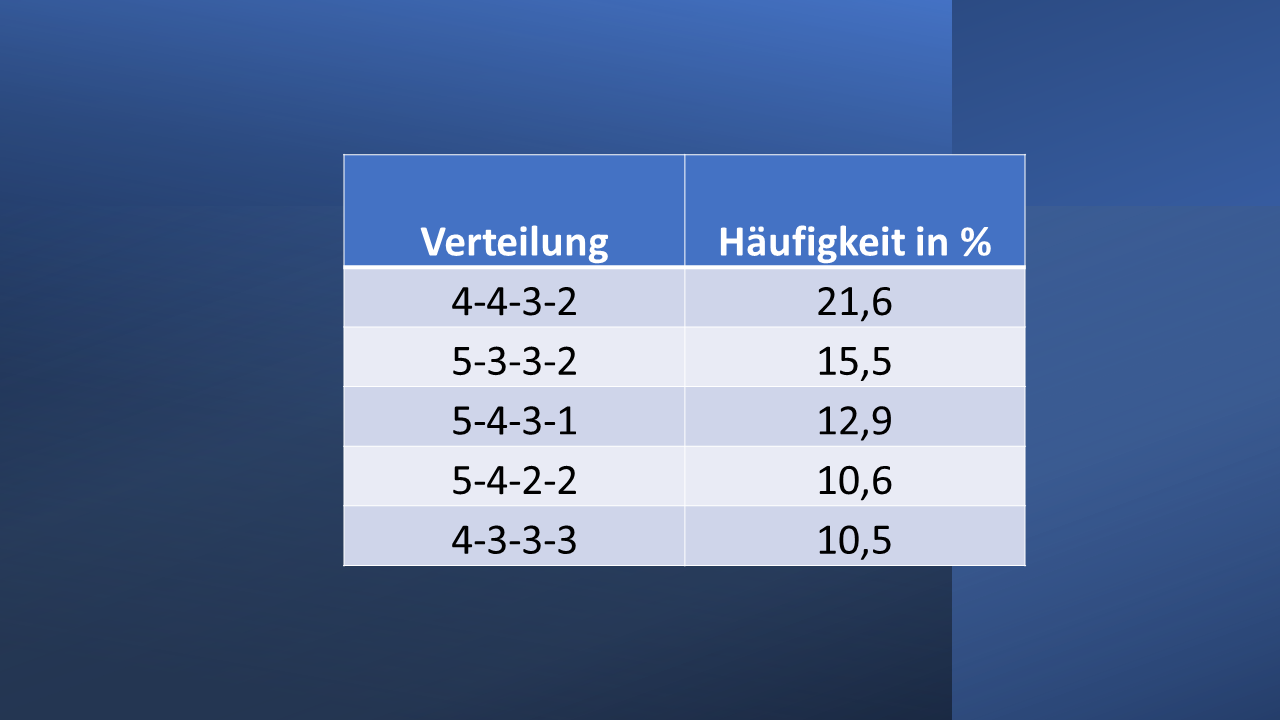
Die folgende Tabelle zeigt die Wahrscheinlichkeit für die Verteilung der Farben in einer Hand. Die Wahrscheinlichkeit für eine 4-4-3-2 Verteilung ist doppelt so hoch wie für eine 4-3-3-3 Verteilung.
Die Originaldaten können bei Bridgehands nachgelesen werden.
Punkte in einer Hand
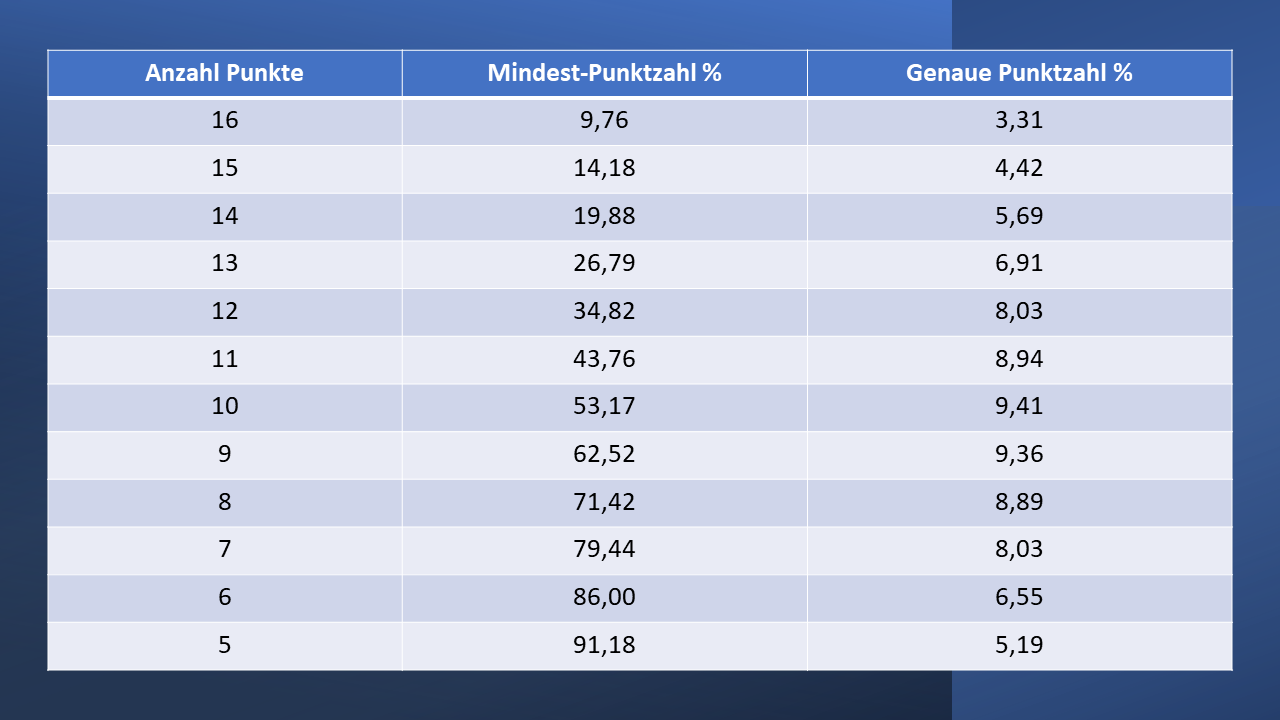
Die folgende Tabelle zeigt, mit welcher Wahrscheinlichkeit man eine bestimmte Anzahl von Punkten in seiner Hand hat. Die zweite Spalte gibt die Wahrscheinlichkeit für eine Mindestpunktzahl an, die dritte Spalte die Wahrscheinlichkeit für eine genaue Punktzahl. Die Wahrscheinlichkeit genau 9 oder 10 Punkte zu halten, ist also am größten.
Die Originaldaten können bei Bridgehands nachgelesen werden.
Anzahl der Karten in einer Farbe
Die folgende Tabelle zeigt die Wahrscheinlichkeiten, wie viele Karten man in einer Farbe bekommt. Die höchste Wahrscheinlichkeit ist für eine 3-er Länge gegeben. Die Originaldaten können bei Bridgehands nachgelesen werden.

Anzahl Kontrollen
Die Wahrscheinlichkeit für die Anzahl der Kontrollen ist abhängig von der Punktzahl einer Hand. Ass zählt als 2 Kontrollen, König als 1 Kontrolle. Bei einer Hand mit 12 Figurenpunkten hat man also mit einer Wahrscheinlichkeit von 42% 4 Kontrollen, d.h. entweder 2 Asse oder 1 Ass und 2 Könige oder 4 Könige. Die Originaldaten können bei Bridgehands nachgelesen werden.

